7 de Mayo 2006
Polinomios por la espalda
Un brazo robot se plantea con frecuencia, para su funcionamiento, el "problema cinemático": si mi hombro está doblado en un ángulo θ1 , y mi codo en un ángulo θ2 , ¿donde está mi mano?.
Con un poco de trigonometría, sabiendo lo que le mide el brazo y el antebrazo, el robot lo resuelve en un momento. (Es un ejercio para el lector que se acuerde de la fórmula del coseno de la suma... Juancho va por ti, ja, ja...)
Más complicado es el "problema cinemático inverso": si quiero poner mi mano en cierto punto ¿que ángulos tengo que poner en mi brazo y en mi codo?. Nito puede demostrar que, si el robot esta en el punto (0,0), con brazo y antebrazo de un metro de largo, y el punto donde quiere poner la mano es (a,b), el seno del ángulo en el hombro tiene que satisfacer lo siguiente (x=sen(θ1) ):
4(a2+b2)x2 -4(a2b +b3)x +(a2+b2) -4a2 = 0
Que como es un polinomio de grado dos en x, hay dos soluciones (para a y b cercanos al origen).
Osea, que hay dos maneras de rascarse la espalda cuando te pica un punto:
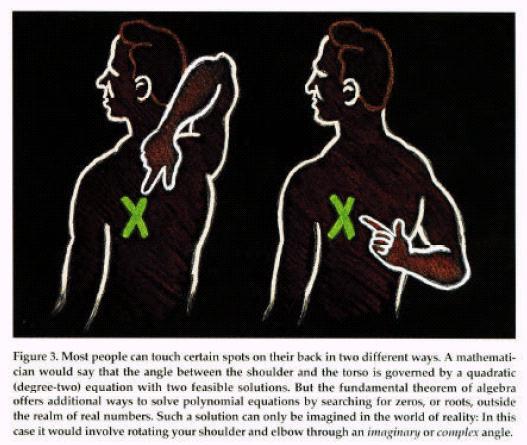
Y también: un punto situado fuera del alcance (2 metros en el caso del robot) no tiene solución real porque el discriminante de la anterior ecuación es negativo. De ahí que por bajito que uno sea, si puede girar su codo un ángulo de seno complejo puede llegar tan alto como quiera.
(Símbolos ♣ √ ℵ en html)
(El escritor del artículo poniendo la mano en un punto (a,b))
Escrito por juanlu a las 7 de Mayo 2006 a las 10:07 PM